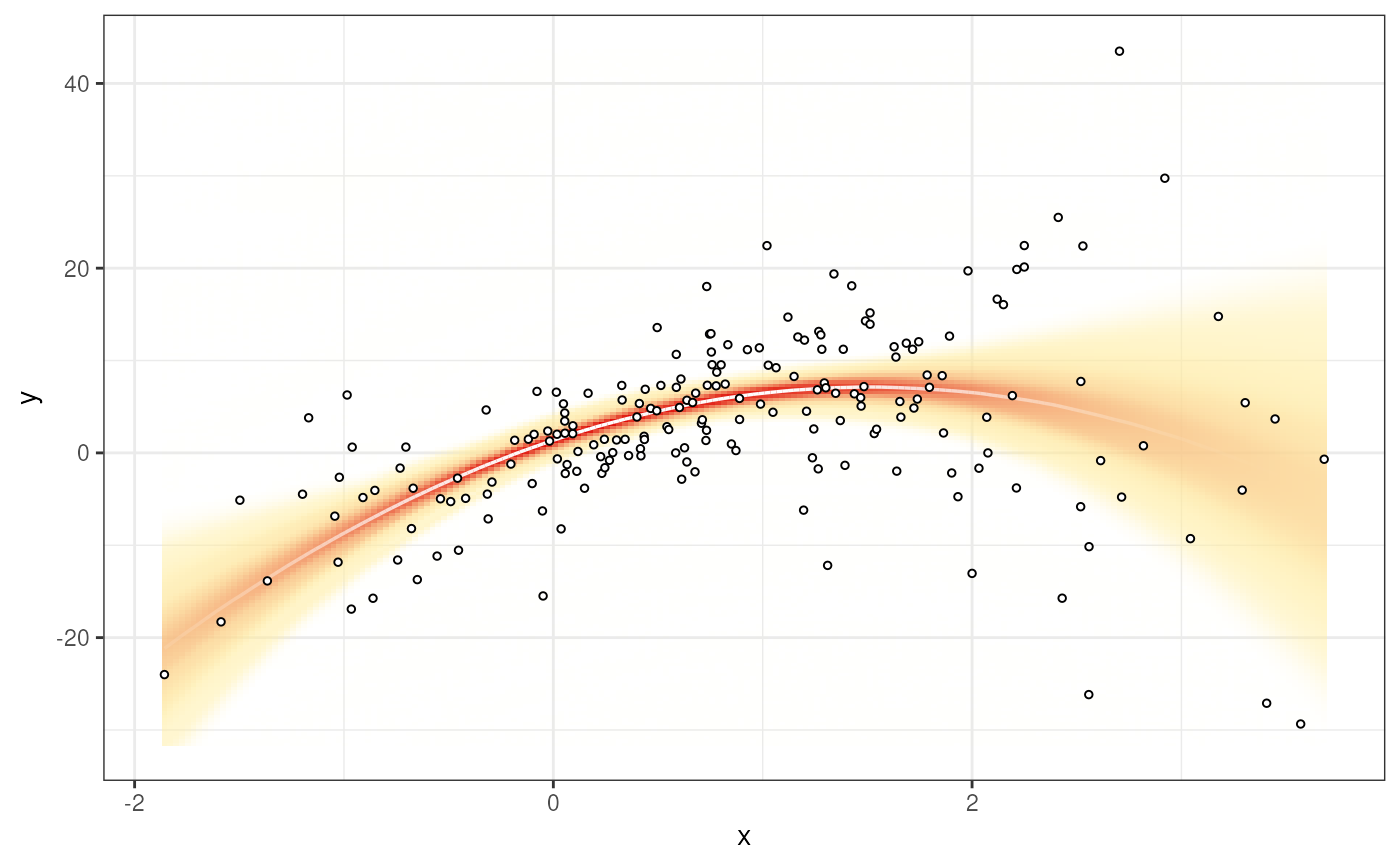
Visually weighted regression / Watercolor plots
Usage
vwReg(
formula,
data,
title = "",
B = 1000,
shade = TRUE,
shade.alpha = 0.1,
spag = FALSE,
spag.color = "darkblue",
mweight = TRUE,
show.lm = FALSE,
show.median = TRUE,
median.col = "white",
shape = 21,
show.CI = FALSE,
method = stats::loess,
bw = FALSE,
slices = 200,
palette = (grDevices::colorRampPalette(c("#FFEDA0", "#DD0000"), bias = 2))(20),
ylim = NULL,
quantize = "continuous",
add = FALSE,
...
)Arguments
- formula
variables to plot. See examples
- data
data frame containing all variables used in formula
- title
passed on to ggplot
- B
= number bootstrapped smoothers
- shade
plot the shaded confidence region?
- shade.alpha
should the CI shading fade out at the edges? (by reducing alpha; 0 = no alpha decrease, 0.1 = medium alpha decrease, 0.5 = strong alpha decrease)
- spag
plot spaghetti lines?
- spag.color
color of spaghetti lines
- mweight
should the median smoother be visually weighted?
- show.lm
should the linear regression line be plotted?
- show.median
should the median smoother be plotted?
- median.col
color of the median smoother
- shape
shape of points
- show.CI
should the 95% CI limits be plotted?
- method
the fitting function for the spaghettis; default: loess
- bw
= TRUE: define a default b&w-palette
- slices
number of slices in x and y direction for the shaded region. Higher numbers make a smoother plot, but takes longer to draw. I wouldn'T go beyond 500
- palette
provide a custom color palette for the watercolors
- ylim
restrict range of the watercoloring
- quantize
either 'continuous', or 'SD'. In the latter case, we get three color regions for 1, 2, and 3 SD (an idea of John Mashey)
- add
if add == FALSE, a new ggplot is returned. If add == TRUE, only the elements are returned, which can be added to an existing ggplot (with the '+' operator)
- ...
further parameters passed to the fitting function, in the case of loess, for example, 'span = .9', or 'family = 'symmetric”
Details
Idea: Solomon Hsiang, with additional ideas from many blog commenters Details: http://www.nicebread.de/visually-weighted-regression-in-r-a-la-solomon-hsiang/ http://www.nicebread.de/visually-weighted-watercolor-plots-new-variants-please-vote/
Examples
# build a demo data set
set.seed(1)
x <- rnorm(200, 0.8, 1.2)
e <- rnorm(200, 0, 3)*(abs(x)^1.5 + .5) + rnorm(200, 0, 4)
e2 <- rnorm(200, 0, 5)*(abs(x)^1.5 + .8) + rnorm(200, 0, 5)
y <- 8*x - x^3 + e
y2 <- 20 + 3*x + 0.6*x^3 + e2
df <- data.frame(x, y, y2)
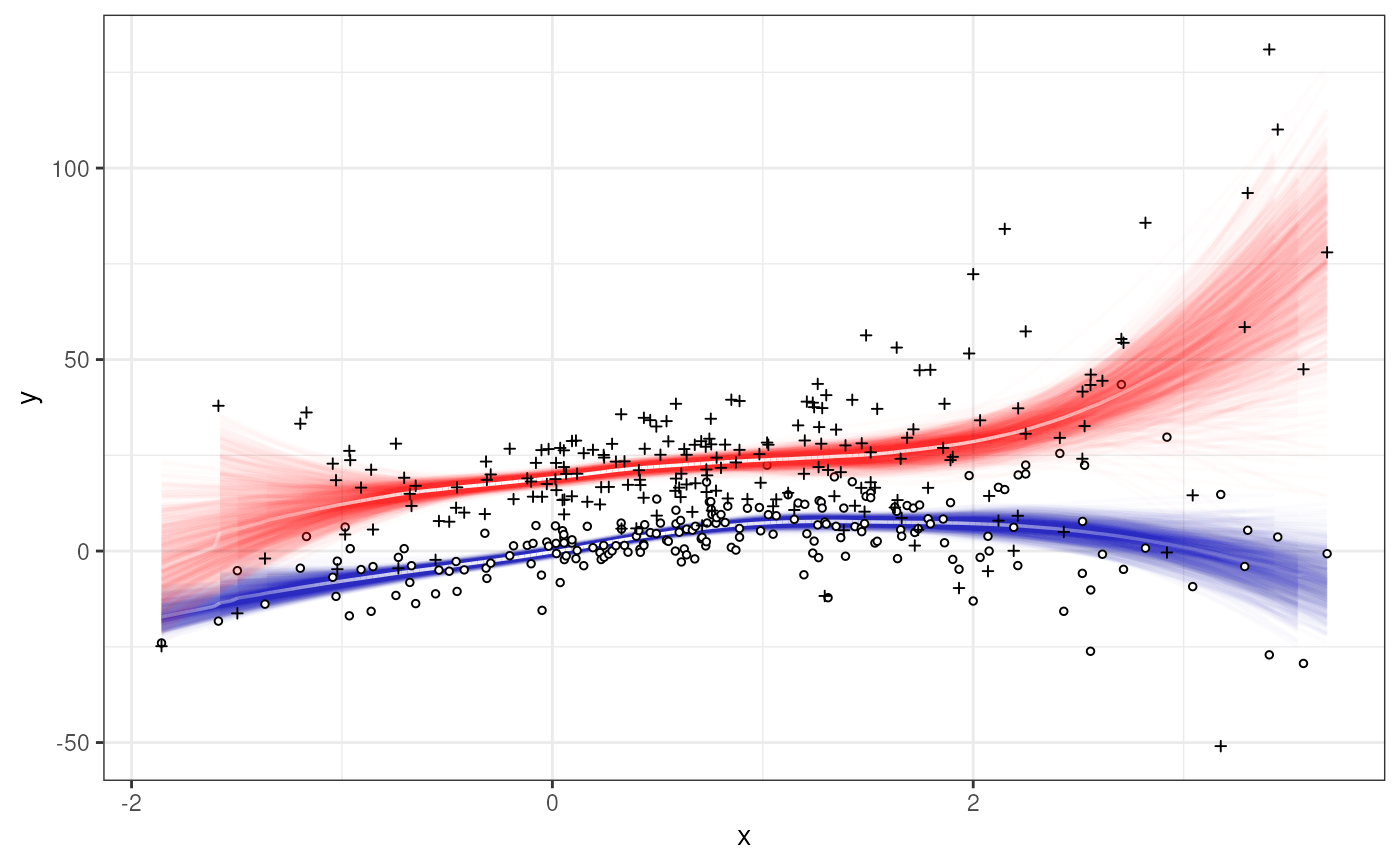
p1 <- vwReg(y~x, df, spag=TRUE, shade=FALSE)
#> [1] "Computing boostrapped smoothers ..."
#> [1] "Build ggplot figure ..."
p2 <- vwReg(y2~x, df, add=TRUE, spag=TRUE, shade=FALSE, spag.color='red', shape=3)
#> [1] "Computing boostrapped smoothers ..."
#> [1] "Build ggplot figure ..."
p3 <- p1 + p2
p3
#> Warning: Removed 6924 rows containing missing values or values outside the scale range
#> (`geom_path()`).
#> Warning: Removed 7020 rows containing missing values or values outside the scale range
#> (`geom_path()`).
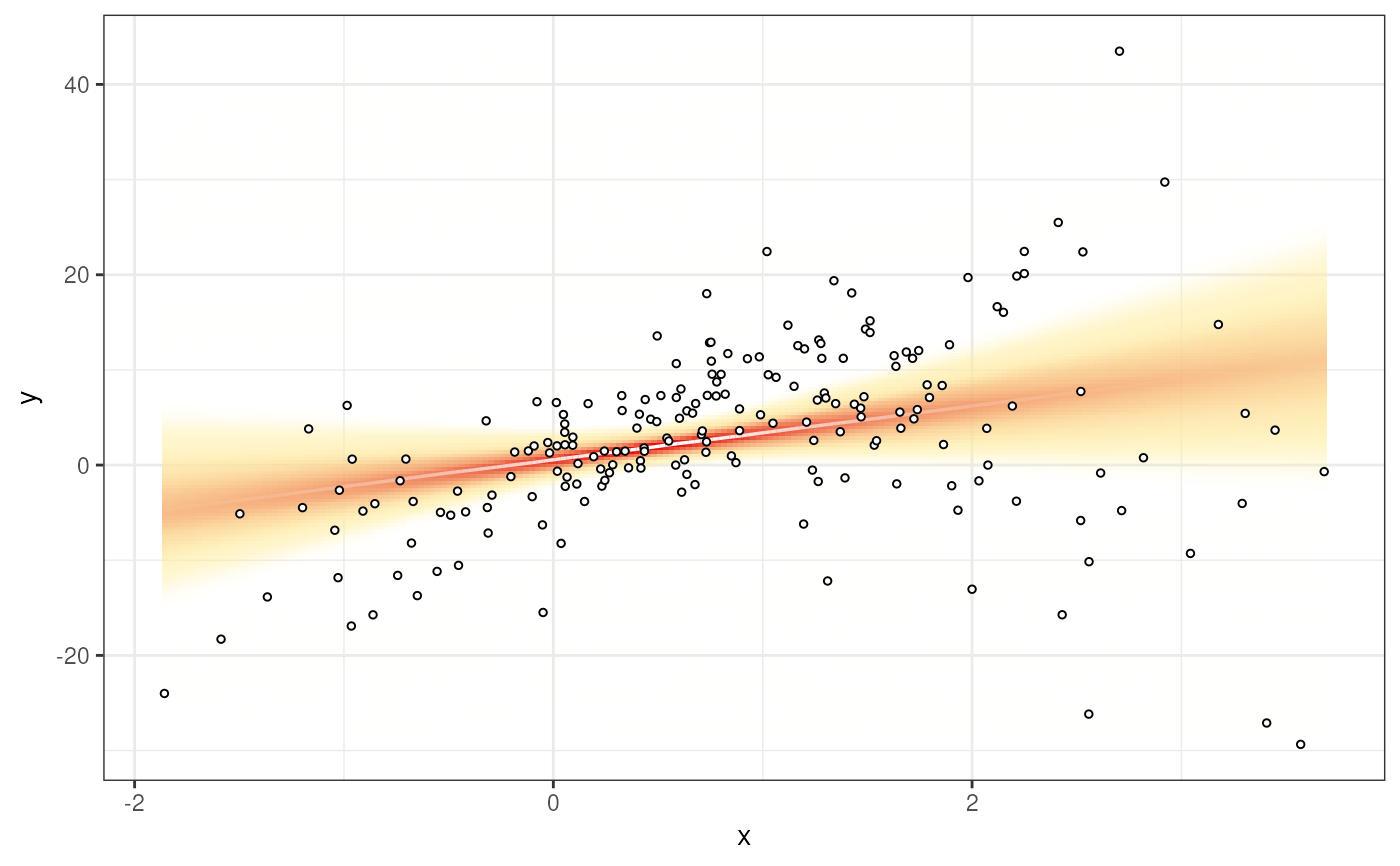
y <- x + x^2 + runif(200, 0, 0.4)
vwReg(y ~ x, df, method=lm)
#> [1] "Computing boostrapped smoothers ..."
#> [1] "Computing density estimates for each vertical cut ..."
#>
|
| | 0%
|
|= | 1%
|
|= | 2%
|
|== | 2%
|
|== | 3%
|
|== | 4%
|
|=== | 4%
|
|==== | 5%
|
|==== | 6%
|
|===== | 6%
|
|===== | 7%
|
|===== | 8%
|
|====== | 8%
|
|====== | 9%
|
|======= | 10%
|
|======== | 11%
|
|======== | 12%
|
|========= | 12%
|
|========= | 13%
|
|========= | 14%
|
|========== | 14%
|
|========== | 15%
|
|=========== | 16%
|
|============ | 16%
|
|============ | 17%
|
|============ | 18%
|
|============= | 18%
|
|============= | 19%
|
|============== | 20%
|
|=============== | 21%
|
|=============== | 22%
|
|================ | 22%
|
|================ | 23%
|
|================ | 24%
|
|================= | 24%
|
|================== | 25%
|
|================== | 26%
|
|=================== | 26%
|
|=================== | 27%
|
|=================== | 28%
|
|==================== | 28%
|
|==================== | 29%
|
|===================== | 30%
|
|====================== | 31%
|
|====================== | 32%
|
|======================= | 32%
|
|======================= | 33%
|
|======================= | 34%
|
|======================== | 34%
|
|======================== | 35%
|
|========================= | 36%
|
|========================== | 36%
|
|========================== | 37%
|
|========================== | 38%
|
|=========================== | 38%
|
|=========================== | 39%
|
|============================ | 40%
|
|============================= | 41%
|
|============================= | 42%
|
|============================== | 42%
|
|============================== | 43%
|
|============================== | 44%
|
|=============================== | 44%
|
|================================ | 45%
|
|================================ | 46%
|
|================================= | 46%
|
|================================= | 47%
|
|================================= | 48%
|
|================================== | 48%
|
|================================== | 49%
|
|=================================== | 50%
|
|==================================== | 51%
|
|==================================== | 52%
|
|===================================== | 52%
|
|===================================== | 53%
|
|===================================== | 54%
|
|====================================== | 54%
|
|====================================== | 55%
|
|======================================= | 56%
|
|======================================== | 56%
|
|======================================== | 57%
|
|======================================== | 58%
|
|========================================= | 58%
|
|========================================= | 59%
|
|========================================== | 60%
|
|=========================================== | 61%
|
|=========================================== | 62%
|
|============================================ | 62%
|
|============================================ | 63%
|
|============================================ | 64%
|
|============================================= | 64%
|
|============================================== | 65%
|
|============================================== | 66%
|
|=============================================== | 66%
|
|=============================================== | 67%
|
|=============================================== | 68%
|
|================================================ | 68%
|
|================================================ | 69%
|
|================================================= | 70%
|
|================================================== | 71%
|
|================================================== | 72%
|
|=================================================== | 72%
|
|=================================================== | 73%
|
|=================================================== | 74%
|
|==================================================== | 74%
|
|==================================================== | 75%
|
|===================================================== | 76%
|
|====================================================== | 76%
|
|====================================================== | 77%
|
|====================================================== | 78%
|
|======================================================= | 78%
|
|======================================================= | 79%
|
|======================================================== | 80%
|
|========================================================= | 81%
|
|========================================================= | 82%
|
|========================================================== | 82%
|
|========================================================== | 83%
|
|========================================================== | 84%
|
|=========================================================== | 84%
|
|============================================================ | 85%
|
|============================================================ | 86%
|
|============================================================= | 86%
|
|============================================================= | 87%
|
|============================================================= | 88%
|
|============================================================== | 88%
|
|============================================================== | 89%
|
|=============================================================== | 90%
|
|================================================================ | 91%
|
|================================================================ | 92%
|
|================================================================= | 92%
|
|================================================================= | 93%
|
|================================================================= | 94%
|
|================================================================== | 94%
|
|================================================================== | 95%
|
|=================================================================== | 96%
|
|==================================================================== | 96%
|
|==================================================================== | 97%
|
|==================================================================== | 98%
|
|===================================================================== | 98%
|
|===================================================================== | 99%
|
|======================================================================| 100%
#> [1] "Build ggplot figure ..."
vwReg(y ~ x + I(x^2), df, method=lm)
#> [1] "Computing boostrapped smoothers ..."
#> [1] "Computing density estimates for each vertical cut ..."
#>
|
| | 0%
|
|= | 1%
|
|= | 2%
|
|== | 2%
|
|== | 3%
|
|== | 4%
|
|=== | 4%
|
|==== | 5%
|
|==== | 6%
|
|===== | 6%
|
|===== | 7%
|
|===== | 8%
|
|====== | 8%
|
|====== | 9%
|
|======= | 10%
|
|======== | 11%
|
|======== | 12%
|
|========= | 12%
|
|========= | 13%
|
|========= | 14%
|
|========== | 14%
|
|========== | 15%
|
|=========== | 16%
|
|============ | 16%
|
|============ | 17%
|
|============ | 18%
|
|============= | 18%
|
|============= | 19%
|
|============== | 20%
|
|=============== | 21%
|
|=============== | 22%
|
|================ | 22%
|
|================ | 23%
|
|================ | 24%
|
|================= | 24%
|
|================== | 25%
|
|================== | 26%
|
|=================== | 26%
|
|=================== | 27%
|
|=================== | 28%
|
|==================== | 28%
|
|==================== | 29%
|
|===================== | 30%
|
|====================== | 31%
|
|====================== | 32%
|
|======================= | 32%
|
|======================= | 33%
|
|======================= | 34%
|
|======================== | 34%
|
|======================== | 35%
|
|========================= | 36%
|
|========================== | 36%
|
|========================== | 37%
|
|========================== | 38%
|
|=========================== | 38%
|
|=========================== | 39%
|
|============================ | 40%
|
|============================= | 41%
|
|============================= | 42%
|
|============================== | 42%
|
|============================== | 43%
|
|============================== | 44%
|
|=============================== | 44%
|
|================================ | 45%
|
|================================ | 46%
|
|================================= | 46%
|
|================================= | 47%
|
|================================= | 48%
|
|================================== | 48%
|
|================================== | 49%
|
|=================================== | 50%
|
|==================================== | 51%
|
|==================================== | 52%
|
|===================================== | 52%
|
|===================================== | 53%
|
|===================================== | 54%
|
|====================================== | 54%
|
|====================================== | 55%
|
|======================================= | 56%
|
|======================================== | 56%
|
|======================================== | 57%
|
|======================================== | 58%
|
|========================================= | 58%
|
|========================================= | 59%
|
|========================================== | 60%
|
|=========================================== | 61%
|
|=========================================== | 62%
|
|============================================ | 62%
|
|============================================ | 63%
|
|============================================ | 64%
|
|============================================= | 64%
|
|============================================== | 65%
|
|============================================== | 66%
|
|=============================================== | 66%
|
|=============================================== | 67%
|
|=============================================== | 68%
|
|================================================ | 68%
|
|================================================ | 69%
|
|================================================= | 70%
|
|================================================== | 71%
|
|================================================== | 72%
|
|=================================================== | 72%
|
|=================================================== | 73%
|
|=================================================== | 74%
|
|==================================================== | 74%
|
|==================================================== | 75%
|
|===================================================== | 76%
|
|====================================================== | 76%
|
|====================================================== | 77%
|
|====================================================== | 78%
|
|======================================================= | 78%
|
|======================================================= | 79%
|
|======================================================== | 80%
|
|========================================================= | 81%
|
|========================================================= | 82%
|
|========================================================== | 82%
|
|========================================================== | 83%
|
|========================================================== | 84%
|
|=========================================================== | 84%
|
|============================================================ | 85%
|
|============================================================ | 86%
|
|============================================================= | 86%
|
|============================================================= | 87%
|
|============================================================= | 88%
|
|============================================================== | 88%
|
|============================================================== | 89%
|
|=============================================================== | 90%
|
|================================================================ | 91%
|
|================================================================ | 92%
|
|================================================================= | 92%
|
|================================================================= | 93%
|
|================================================================= | 94%
|
|================================================================== | 94%
|
|================================================================== | 95%
|
|=================================================================== | 96%
|
|==================================================================== | 96%
|
|==================================================================== | 97%
|
|==================================================================== | 98%
|
|===================================================================== | 98%
|
|===================================================================== | 99%
|
|======================================================================| 100%
#> [1] "Build ggplot figure ..."
